Adaptive grammar

An adaptive grammar is a formal grammar that explicitly provides mechanisms within the formalism to allow its own production rules to be manipulated.

Contents

Overview

John N. Shutt defines adaptive grammars as follows:

ADAPTIVE GRAMMAR MODEL: A grammatical formalism that allows rule sets (aka sets of production rules) to be explicitly manipulated within a grammar.[1]

Types of manipulation include rule addition, deletion, and modification.

Early history

The first description of grammar adaptivity (though not under that name) in the literature is generally[2][3][4] taken to be in a paper by Alfonso Caracciolo di Forino published in 1963.[5] The next generally accepted reference to an adaptive formalism (extensible context-free grammars) came from Wegbreit in 1970[6] in the study of extensible programming languages, followed by the dynamic syntax of Hanford and Jones in 1973.[7]

Collaborative efforts

Until fairly recently, much of the research into the formal properties of adaptive grammars was uncoordinated between researchers, only first being summarized by Henning Christiansen in 1990[2] in response to a paper in ACM SIGPLAN Notices by Boris Burshteyn.[8] The Department of Engineering at the University of São Paulo has its Adaptive Languages and Techniques Laboratory, specifically focusing on research and practice in adaptive technologies and theory. The LTA also maintains a page naming researchers in the field.[9]

Terminology and taxonomy

While early efforts made reference to dynamic syntax[7] and extensible,[6] modifiable,[10] dynamic,[11] and adaptable[2][12] grammars, more recent usage has tended towards the use of the term adaptive (or some variant such as adaptativa,[13][14] depending on the publication language of the literature).[3] Iwai refers to her formalism as adaptive grammars,[13] but this specific use of simply adaptive grammars is not typically currently used in the literature without name qualification. Moreover, no standardization or categorization efforts have been undertaken between various researchers, although several have made efforts in this direction.[3][4]

The Shutt classification (and extensions)

Shutt categorizes adaptive grammar models into two main categories:[3][15]

Jackson refines Shutt's taxonomy, referring to changes over time as global and changes over space as local, and adding a hybrid time-space category:[4]

Adaptive formalisms in the literature

Adaptive formalisms may be divided into two main categories: full grammar formalisms (adaptive grammars), and adaptive machines, upon which some grammar formalisms have been based.

Adaptive grammar formalisms

The following is a list (by no means complete) of grammar formalisms that, by Shutt's definition above, are considered to be (or have been classified by their own inventors as being) adaptive grammars. They are listed in their historical order of first mention in the literature.

Extensible Context-Free Grammars (Wegbreit)

Described in Wegbreit's doctoral dissertation in 1970,[6] an extensible context-free grammar consists of a context-free grammar whose rule set is modified according to instructions output by a finite state transducer when reading the terminal prefix during a leftmost derivation. Thus, the rule set varies over position in the generated string, but this variation ignores the hierarchical structure of the syntax tree. Extensible context-free grammars were classified by Shutt as imperative.[3]

Christiansen Grammars (Christiansen)

First introduced in 1985 as Generative Grammars[16] and later more elaborated upon,[17] Christiansen grammars[18] are an adaptive extension of attribute grammars. Christiansen grammars were classified by Shutt as declarative.[3]

The redoubling language 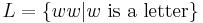L = \{ww | w \mbox{ is a letter}\} is demonstrated as follows:[17]

<program↓G>       →   <dcl↓G↑w> <body↓{w-rule}>

where w-rule  =
<body↓G’>         →   w

<dcl↓G↑ch•w>     →   <char↓G↑ch> <dcl↓G↑w>
<dcl↓G↑<>>       →   <ε>
<char↓G↑a>       →   a

Bottom-Up Modifiable Grammars, Top-Down Modifiable Grammars, and USSA (Burshteyn)

First introduced in May 1990[8] and later expanded upon in December 1990,[10] modifiable grammars explicitly provide a mechanism for the addition and deletion of rules during a parse. In response to the ACM SIGPLAN Notices responses, Burshteyn later modified his formalism and introduced his adaptive Universal Syntax and Semantics Analyzer (USSA) in 1992.[19] These formalisms were classified by Shutt as imperative.[3]

Recursive Adaptive Grammars (Shutt)

Introduced in 1993, Recursive Adaptive Grammars (RAGs) were an attempt to introduce a Turing powerful formalism that maintained much of the elegance of context-free grammars.[3] Shutt self-classifies RAGs as being a declarative formalism.

Dynamic Grammars (Boullier)

Boullier's dynamic grammars, introduced in 1994,[11] appear to be the first adaptive grammar family of grammars to rigorously introduce the notion of a time continuum of a parse as part of the notation of the grammar formalism itself.[4] Dynamic grammars are a sequence of grammars, with each grammar Gi differing in some way from other grammars in the sequence, over time. Boullier's main paper on dynamic grammars also defines a dynamic parser, the machine that effects a parse against these grammars, and shows examples of how his formalism can handle such things as type checking, extensible languages, polymorphism, and other constructs typically considered to be in the semantic domain of programming language translation.

Adaptive Grammars (Iwai)

The work of Iwai in 2000[13] takes the adaptive automata of Neto[20] further by applying adaptive automata to context-sensitive grammars. Iwai's adaptive grammars (note the qualifier by name) allow for three operations during a parse: ? query (similar in some respects to a syntactic predicate, but tied to inspection of rules from which modifications are chosen), + addition, and - deletion (which it shares with its predecessor adaptive automata).

§-Calculus (Jackson)

Introduced in 2000[21] and most fully discussed in 2006,[4] the §-Calculus (§ here pronounced meta-ess) allows for the explicit addition, deletion, and modification of productions within a grammar, as well as providing for syntactic predicates. This formalism is self-classified by its creator as both imperative and adaptive, or, more specifically, as a time-space adaptive grammar formalism, and was further classified by others as being an analytic formalism.[14][22]

The redoubling language 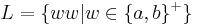L = \{ww | w \in \{a,b\}^%2B\} is demonstrated as follows:

grammar ww {
 S ::= #phi(A.X<-"") R;
 R ::= $C('[ab]') #phi(A.X<-A.X C) #phi(N<=A.X) N | R;
};

(Note on notation: In the above example, the #phi(...) statements identify the points in the production R that modify the grammar explicitly. #phi(A.X<-A.X C) represents a global modification (over time) and the #phi(N<=A.X) statement identifies a local modification (over space). The #phi(A.X<-"") statement in the S production effectively declares a global production called A.X by placing the empty string into that production before its reference by R.)

Adaptive Devices (Neto & Pistori)

First described by Neto in 2001,[23] adaptive devices were later enhanced and expanded upon by Pistori in 2003.[24]

Adapser (Carmi)

In 2002,[25] Adam Carmi introduced an LALR(1)-based adaptive grammar formalism known as Adapser. Specifics of the formalism do not appear to have been released.

Adaptive CFGs with Appearance Checking (Bravo)

In 2004,[14] César Bravo introduced the notion of merging the concept of appearance checking[26] with adaptive context-free grammars, a restricted form of Iwai's adaptive grammars,[13] showing these new grammars, called Adaptive CFGs with Appearance Checking to be Turing powerful.

Adaptive machine formalisms

The formalisms listed below, while not grammar formalisms, either serve as the basis of full grammar formalisms, or are included here because they are adaptive in nature. They are listed in their historical order of first mention in the literature.

Self-Modifying Finite State Automata (Shutt & Rubinstein)
Introduced in 1994 by Shutt and Rubinstein,[27] Self-Modifying Finite State Automata (SMFAs) are shown to be, in a restricted form, Turing powerful.
Adaptive Automata (Neto)
In 1994,[20] Neto introduced the machine he called a structured pushdown automaton, the core of adaptive automata theory as pursued by Iwai,[13] Pistori,[24] Bravo[14] and others. This formalism allows for the operations of inspection (similar to syntactic predicates, as noted above relating to Iwai's adaptive grammars), addition, and deletion of rules.

See also

References and notes

  1. ^ Shutt, John N., "What is an Adaptive Grammar?" Web page dated 28 March 2001, at the URL: http://www.cs.wpi.edu/~jshutt/adapt/adapt.html
  2. ^ a b c Christiansen, Henning, "A Survey of Adaptable Grammars," ACM SIGPLAN Notices, Vol. 25 No. 11, pp. 35-44, Nov. 1990.
  3. ^ a b c d e f g h Shutt, John N., Recursive Adaptable Grammars, Master’s Thesis, Worcester Polytechnic Institute, 1993. (16 December 2003 emended revision.)
  4. ^ a b c d e Jackson, Quinn Tyler, Adapting to Babel: Adaptivity and Context-Sensitivity in Parsing, Ibis Publications, Plymouth, Massachusetts, March 2006.
  5. ^ Caracciolo di Forino, Alfonso, "Some Remarks on the Syntax of Symbolic Programming Languages," Communications of the ACM, Vol. 6, No. 8., pp. 456-460, August 1963.
  6. ^ a b c Wegbreit, Ben, Studies in Extensible Programming Languages, ESD-TR-70-297, Harvard University, Cambridge, Massachusetts, May 1970. In book form, Garland Publishing, Inc., New York, 1980.
  7. ^ a b Hanford, K.V. & Jones, C.B., "Dynamic Syntax: A Concept for the Definition of the Syntax of Programming Languages," Annual Review in Automatic Programming 7, Pergamon Press, Oxford, pp. 115-142, 1973.
  8. ^ a b Burshteyn, Boris. "On the Modification of the Formal Grammar at Parse Time", ACM SIGPLAN Notices, Vol. 25 No. 5, pp. 117-123, May 1990.
  9. ^ http://www.pcs.usp.br/~lta/union/index.php?cp=4&categoria=28
  10. ^ a b Burshteyn, Boris, "Generation and Recognition of Formal Languages by Modifiable Grammars," ACM SIGPLAN Notices, Vol. 25 No. 12, pp. 45-53, December 1990.
  11. ^ a b Boullier, Pierre, "Dynamic Grammars and Semantic Analysis," INRIA Research Report No. 2322, August 1994.
  12. ^ John Shutt originally called his Recursive Adaptive Grammars by the name Recursive Adaptable Grammars, and notes his change to adaptive at this URL: John Shutt's MS Thesis.
  13. ^ a b c d e Iwai, Margarete Keiko, Um formalismo gramatical adaptativo para linguagens dependentes de contexto, Doctoral thesis, Department of Engineering, University of São Paulo, Brazil, January 2000.
  14. ^ a b c d Bravo, César, Grámmaticas Livres de Contexto Adaptativas com verificação de aparência, Doctoral thesis, Department of Electrical Engineering, University of São Paulo, January 2004.
  15. ^ Shutt, John N., "Imperative Adaptive Grammars" Web page dated 28 March 2001, at the URL: http://web.cs.wpi.edu/~jshutt/adapt/imperative.html
  16. ^ Christiansen, Henning, "Syntax, Semantics, and Implementation Strategies for Programming Languages with Powerful Abstraction Mechanisms," Proceedings of the 18th Hawaii International Conference on System Sciences, Vol. 2, pp. 57-66, 1985.
  17. ^ a b Christiansen, Henning, "The Syntax and Semantics of Extensible Languages," Datalogiske skrifter 14, Roskilde University, 1988.
  18. ^ Apparently dubbed such by Shutt.
  19. ^ Burshteyn, Boris, "USSA–Universal Syntax and Semantics Analyzer," ACM SIGPLAN Notices, Vol. 27 No. 1, pp. 42-60, January 1992.
  20. ^ a b Neto, João Jose, "Adaptive Automata for Context-Sensitive Languages," ACM SIGPLAN Notices, Vol. 29 No. 9, pp. 115-124, September 1994.
  21. ^ Jackson, Quinn Tyler, "Adaptive Predicates in Natural Language Parsing," Perfection, Vol. 1 No. 4, April 2000.
  22. ^ Okhotin, Alexander, Boolean Grammars: Expressive Power and Algorithms, Doctoral thesis, School of Computing, Queens University, Kingston, Ontario, August 2004.
  23. ^ Neto, João Jose, "Adaptive Rule-Driven Devices: General Formulation and Case Study," B. W. Watson, D. Wood (Eds.): Implementation and Application of Automata 6th International Conference, CIAA 2001, Lecture Notes in Computer Science, Vol. 2494, Pretoria, South Africa, Springer-Verlag, pp. 234–250, 23–25 July 2001.
  24. ^ a b Pistori, Hemerson, Tecnologia Adaptativa em Engenharia de Computação: Estado da Arte e Aplicações, Doctoral thesis, Department of Electrical Engineering, University of São Paulo, 2003.
  25. ^ Carmi, Adam, "Adapser: An LALR(1) Adaptive Parser," The Israeli Workshop on Programming Languages & Development Environments, Haifa, Israel, 1 July 2002.
  26. ^ Salomaa, Arto, Formal Languages, Academic Press, 1973.
  27. ^ Shutt, John & Rubinstein, Roy, "Self-Modifying Finite Automata," in B. Pehrson and I. Simon, editors, Technology and Foundations: Information Processing ‘94 Vol. I: Proceedings of 13th IFIP World Computer Congress, Amsterdam: North-Holland, pp. 493-498, 1994.

External links

Scholarly Conferences Specifically Covering Adaptive Aspects of Formal Languages
Post-Secondary Level Courses Covering Adaptive Grammar
List of Researchers in Adaptive Grammars